Packed Data support in Haskell

This blog post aims to be a short and accessible summary of a paper that will be published at ECOOP 2025, titled Type-safe and portable support for packed data.

Introduction: Packed Data

When programs want to persist data or send it over the network, they need to serialise it (e.g. to JSON or XML). On the other hand, when a program receives data from the network or reads it from a file, data needs to be deserialised.

flowchart LR
        Server(["Server"])
        Server --> SD["Serialise"]
        SD -- Network --- RD["Deserialise"]
        RD --> Client(["Client"])

These de/serialisation steps are necessary because we cannot use the in-memory representation/layout of the data in a file or when sending it over the network, mainly because of the pointers it may contain.

Consequently, de/serialising data has a cost: it takes time, and the serialised version of the data is usually bigger than its in-memory representation. In the context of systems that interact through the network, it leads to larger payloads to send, and thus slower transfer times.

Now, what if we didn’t have to serialise the data before sending it to a client, and what if the client could use the data from the network as-is, without any marshalling steps? We could save some time, on both the server and client side.

Introducing the ‘packed’ data format, a binary format that allows using data as it is, without the need for a deserialisation step. A notable perk of this format is that traversals on packed trees is proven to be faster than on ‘unpacked’ trees: as the fields of data structures are inlines, there are no pointer jumps, thus making the most of the L1 cache.

To better understand how it looks like, here is a representation of a tree in memory that uses pointers. N represents nodes, and L represents leaves. Numbers are the tree’s data, and dots and arrows are pointers.

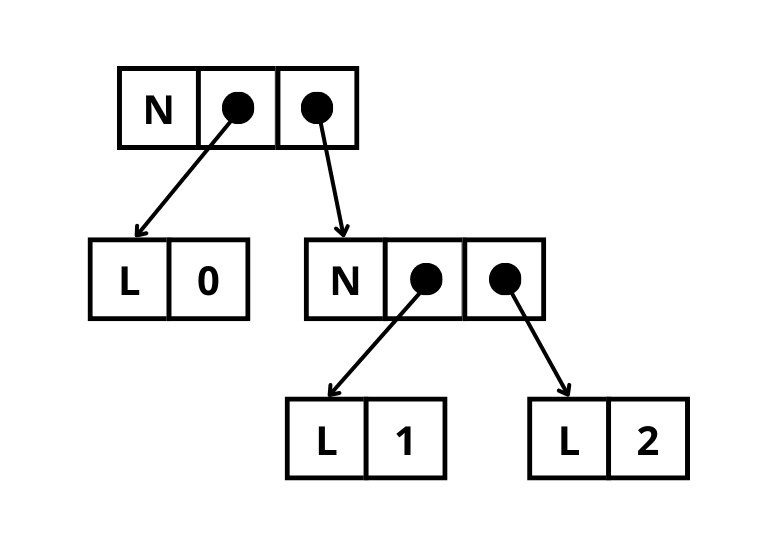Pointer-based tree layout in memory

Here is what a packed tree looks like in memory.

Packed tree layout in memory

A few projects use or leverage this ‘packed’ approach. For example, Cap’n Proto¹ is a popular library that allows packing data (i.e. build a binary buffer containing the data), using that buffer as-is (e.g. traverse it and ‘unpack’ fields of a structure). However, no languages support packed data natively. Haskell does support compact normal forms (CNF), but the Compact data type does not allow using (e.g. deconstructing) packed values. We should note the existence of Gibbon, a research compiler that accepts functional programs and generates programs that use packed data natively.

Unfortunately the use of packed data is limited to research projects, probably because it’s kinda hard to support it.

In this post, I will introduce the packed-data Haskell library. It allows packing and unpacking data, as well as traversing packed data as-is (with a custom case function), with no marshalling step or compiler mods, thanks to the power of types. As far as we are aware, this is on of the first effort to bring support for packed data using only the host language’s type-system, meta-programming (Template Haskell) with no compiler modifications.

The library, its features and its API

Using Template Haskell, packed-data generates all the necessary code so that one can, for any type² :

• pack data (i.e. serialise the data into a binary format)
• unpack data (i.e. deserialise the data from that binary format)
• traverse the data, thanks to a generated case function that allows pattern matching on a data type’s constructor.

Let’s consider the example of a binary tree:

data Tree a = Leaf a | Node (Tree a) (Tree a)

We can use the following Template Haskell entrypoint (from Data.Packed):

$(mkPacked ''Tree [])

which generates instances of the following classes (defined in Data.Packed as well)

class Packable a where
  write :: a -> NeedsBuilder a r t

class Unpackable a where
  read :: PackedReader '[a] r a

along with the function

caseTree :: (PackedReader '[a] r b) ->
            (PackedReader '[Tree a, Tree a] r b) ->
            (PackedReader '[Tree a] r b)

Ooh, all these types are scary. Don’t worry, we’ll look into them right now.

NeedsBuilder

To build packed data, we use an intermediary buffer, through its phantom type parameters, can restrict what data it takes as input.

We didn’t come up with that idea, it is heavily inspired by the examples from the Linear Haskell paper¹. The paper’s authors define the Needs type, with two phantom type parameters, p and t, where

• p tells the types of the data the buffer needs before it can be considered as ready or full
• t gives the types of all the data packed in the buffer, once it’s ready (i.e. when p is an empty list)

import Data.ByteString.Builder (Builder)

newtype Needs (p :: [Type]) (t :: [Type]) = Needs Builder

For example, Needs '[Int] '[Tree Int] is an incomplete buffer that needs an Int before we can reify it into a proper packed (Tree Int). On the other hand, Needs '[] '[Char, Char] is ready to be reified, and the produced buffer will contain two Chars.

We expand on that paper’s idea to make the building of the buffers monadic. For example, with Template Haskell, we generate the following code (or something similar) to write a Tree into a Needs

instance Packable Tree where
  write (Leaf n) = do 
    writeTag 0
    write n -- The library provides an instance of Packable Int
  write (Node t1 t2) = do
    writeTag 1
    write t1 -- We call the function recursively
    write t2

The Needs type is just a wrapper around a Data.ByteString.Builder. The buffer is not created when we use the write function³. It’s what finish is for:

finish :: Needs '[] t -> Packed t

Notice how the first type parameter of the input Needs is empty. It ensures that the buffer is full and ready.

The library also provides a shorthand pack function:

pack :: (Packable a) => Packed '[a]
pack  = finish . withEmptyNeeds . write

PackedReader

PackedReader represents reading operations on packed data. It is a monad. More specifically, it’s an indexed one. This means that the ‘state’ of the computation is reflected in its type.

For example, PackedReader '[Int] '[Int, Int] Char reads a single Int in a buffer where the rest of the buffer contains two other Int. This means that we could use that reader with a Packed '[Int, Int, Int], but not a Packed '[Char, Int, Int]. The operation produces a Char.

Why does this monad exist? Under the hood, the PackedReader passes around a Ptr and reads data using peek, in the IO monad. PackedReader abstract away pointer manipulations while also ensuring type-correct reading operations on packed buffers.

What it would look like without `PackedReader`

Here is what a traversal on a packed `Tree` (defined in the next subsection) would look like without the `PackedReader` abstraction. ```haskell getRightMostNodePacked :: Packed (Tree1 Int ': r) -> IO Int getRightMostNodePacked packed = fst <$> go (unsafeForeignPtrToPtr fptr) where (BS fptr _) = fromPacked packed go :: Ptr Word8 -> IO (Int, Ptr Word8) go ptr = do tag <- peek ptr :: IO Word8 case tag of 0 -> do !n <- peek (plusPtr ptr 1) return (n, plusPtr ptr 9) 1 -> do (!_, !r) <- go (plusPtr ptr 1) (!right, !r1) <- go r return (right, r1) _ -> undefined ``` Pretty ugly, innit?

The case function

For each call to mkPacked, a case function for the given type.

For instance, for the Tree ADT, it generates the caseTree function. It takes as many PackedReaders as parameter as there are constructors in Tree. Each PackedReader has a type that matches each constructor’s type:

data Tree a = Leaf a | Node (Tree a) (Tree a)

caseTree :: 
  -- The first PackedReader will only read an 'a', 
  -- as the first constructor has an 'a' 
  (PackedReader '[a] r b) -> 
  -- The second reads two trees
  (PackedReader '[Tree a, Tree a] r b) -> 
  -- The resulting PackedReader reads a 'Tree'
  (PackedReader '[Tree a] r b)

We can use the generated caseTree function to define the instance of Unpackable for Tree:

-- This function is generated by `mkPacked`
instance (Unpackable a) => Unpackable (Tree a) where
  read = caseTree 
    (do 
      n <- read -- 'n' has type Int
      return n
    )
    (do 
      left <- read -- 'left' is a 'Tree a' 
      right <- read -- 'right' is also a 'Tree a'
      return $ Node left right
    )

The second lambda can feel a bit weird at first. You can think of a PackedReader as an operation that moves a cursor within a buffer. Here read unpacks the value at the current cursor’s position, and shifts it to the next packed value.

Indirections

One common challenge with packed data is to access a field in a packed data structure. Since all fields are inlined, we cannot predict the position of a given field in the buffer, as the preceding fields may not have a fixed size (in the case of a recursive data structure, like a tree).

Thus, there are two ways to access a field:

• Traversing the preceding ones. This can lead to dramatic performance issues if these preceding fields are big.
• Prefix each field with an indirection: a number that gives the size of the field it precedes. They allow us to skip over a field though a simple pointer shift. Inpacked-data, we call them FieldSize.

When building packed data, the library automatically inserts these indirections and modifies the signature of the case function so that its PackedReader know that there are FieldSize interspersed in the buffer.

To skip over a value preceded with a FieldSize, we provide the skipwithFieldSize function, which has type PackedReader '[FieldSize, a] r ().

Examples

Here’s what getting the right-most value in a packed tree would look like:

getRightMostNodePacked :: PackedReader '[Tree1 Int] r Int
getRightMostNodePacked =
    caseTree1
        read
        skip R.>> getRightMostNodePacked

Summing the values in the packed tree is similar:

sumPacked :: PackedReader '[Tree1 Int] r Int
sumPacked =
    caseTree1
        read
        ( R.do
            !left <- sumPacked
            !right <- sumPacked
            let !res = left + right
            R.return res
        )

You can find more examples of tree traversals in the package’s repository.

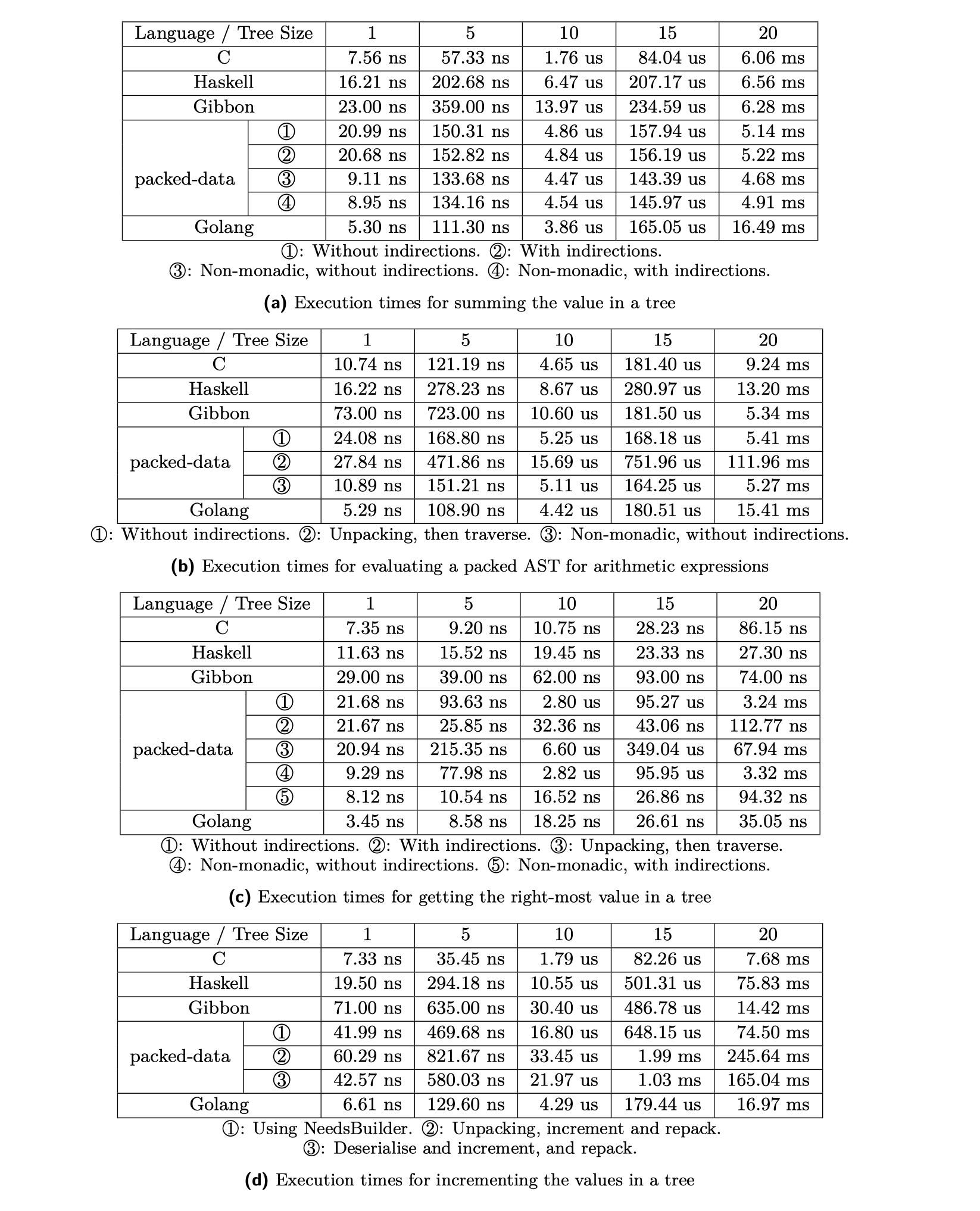
Benchmarks

How fast is all that stuff? To answer that question, we ran benchmarks on simple tree traversals: summing the values in a tree, getting the right-most value in a tree, evaluating an AST for an arithmetic expression, and incrementing the leaves values in a tree.

We compared the execution time of these operations with C, ‘Unpacked’/native Haskell and Gibbon, on trees of sizes between 1 and 20 (for example, a tree of size 5 has 2^5 = 32 leaves, dispatched symmetrically). We noticed the following:

• For summing the values, we notice a small speed-up (20%) compared to ‘unpacked’ Haskell.
• On the other hand, getting the right-most value in the tree is 5 times slower than native Haskell.
• Evaluating the AST is surprisingly faster (2.5x) compared to both Haskell and C.
• Finally, incrementing the values of a packed tree is as fast as incrementing a native, unpacked tree in Haskell. We think this is due to the fact that the ByteString.Builder does only one big memory allocation, while the native operation does one for each node.

The complete benchmark results table

We should note that these benchmark results vary depending on the architecture of the machine’s CPU. ARM CPUs do not enjoy such speed-ups compared to Intel CPUs.

(You can run these benchmarks on your machine, the source code is available on GitHub)

Interpretation of the results

Well, we did get some speed-ups, but it’s not consistent across our benchmark cases.

Using a packed layout should always provide faster traversals, as we avoid jumping using pointers, and make the most of the L1 cache.

We suspect that the monadic approach of the PackedReader leads to some computation overhead due to the intensive use of IO operations (like peek).

For fun, we implemented a non-monadic version of a traversal to get the right-most value in a packed tree. This version does not use PackedReader and uses peek without any abstraction. (The code is available here). It did speed up the traversal (30% faster than the PackedReader), but is still slower (4x) than native Haskell.

This confirms that there is a computing overhead caused by our monadic abstraction of pointer manipulation.

Future work and conclusion

OK, so using only a library, with no compiler modifications, we somewhat managed to leverage the speed-ups allowed by packed data. However, because of its shallow embedding (i.e. it’s just a library), we suffer from computing overhead, which can hardly be bypassed without changing the compiler.

A solution would be to rewrite the library so that PackedReader generates an AST, which would be used to generate C code. Then, using Template Haskell, we could inject an FFI call into the Haskell code, in place of the PackedReader execution. This would allow us to avoid the computing overhead caused by our monadic approach.

I only rely on types to ensure the correctness of reading operations on packed data. I am actually curious to see if this library-based approach would work on other strongly-typed languages like Rust, Scala or maybe even TypeScript.

I talked about servers and clients in the introduction. For web services, it’s common to use JSON. It would be interesting to see if it is possible to use a JSON bytestring as-is on the client-side, without the need for a deserialisation step, using a strongly-types interface like in packed-data.

1. Linear Haskell paper ↩︎ ↩︎²

2. as long as it is not an unboxed type ↩︎

3. We recommend taking a look at the Data.ByteString.Builder module. ↩︎